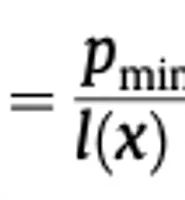[ 논문 ] "On Measuring of Similarity between tree nodes (Gleb Sologub.)" - tree nodes 의 Similarity 구하기

 

" On Measuring of Similarity between tree nodes " 

Abstract 

Hierarchy 개념이 합재되어 있는 tree 에서 두개의 nodes의 Similarity 를 구하는 방법으로는 [1] Path-based , [2] Structure equivalence measures 있다. 하지만 이 두 방법을 직접 tree nodes similarity 를 구하기 위해 적용하면 계산이 망가지고 만다. 따라서 해당 논문에서는 Adjusted path-based similarity measure 방법과 tree nodes 를 binary vector 로 표현하는 새로운 representation을 제시한다. 

 

Path metric 

원래 tree 에서 두개의 nodes의 shortest path 를 보통 path metric 이라 칭한다. 즉 length of the shortest path 이고 식으로는 다음과 같이 표현 할 수 있다. 

 

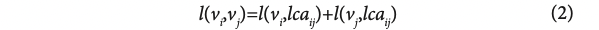
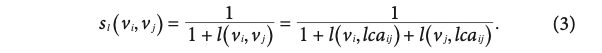
# 예시 

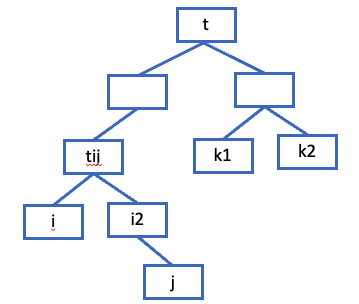
다음 과 같은 Tree 가 있다고 가정을 하였을때, node 'i' 와 'i2' 의 path metric = 2,  'k1' 와 'k2' 의 path metric 또한 2 이다. 즉 그들의 similarity 는 같다고 계산되지만 실제로 k1, k2 보다 I,i2 의 similarity 가 더 높다는 것을 알 수 있다. 

이를 개선하기 위해서 해당 논문에서 adjusted path-based similarity 를 제시하였다. 

 

 

 

 

 

 

 

 

 

Adjusted path-based similarity 

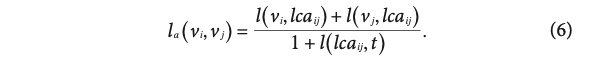
해당 식은 (6)와 같이 표현되며, 곂치는 path와 root와의 거리또한 이용햐여 계산한 것을 볼 수 있다. 따라서 node 'i' 와 'j'의 path metric 은 l (vi, vj) = (1+2) / (1+2) = 1 ,  similarity 는 1 / 2 로 나타낼 수 있다.