| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- pandas
- single cell analysis
- MACS2
- scRNAseq
- scRNAseq analysis
- javascript
- HTML
- CUT&RUN
- matplotlib
- Bioinformatics
- drug muggers
- DataFrame
- 싱글셀 분석
- CSS
- julia
- EdgeR
- drug development
- python matplotlib
- ChIPseq
- single cell
- single cell rnaseq
- github
- 비타민 C
- js
- PYTHON
- Git
- CUTandRUN
- Batch effect
- cellranger
- ngs
- Today
- Total
바이오 대표
[ 논문 ] "Digital Signal Processing" - On the design of maximally incoherent sensing matrics for compressed sensing using orthogonal bases, and its extension for biorthogonal bases case 본문
[ 논문 ] "Digital Signal Processing" - On the design of maximally incoherent sensing matrics for compressed sensing using orthogonal bases, and its extension for biorthogonal bases case
바이오 대표 2022. 1. 24. 23:35
Abstract
Compressed Sensing (CS)는 Nyquist criterion 에 규정되어 있는 것보다 적은 measurements 를 이용하지만 낮은 error 로 sparse signals 를 reconstruct (복구) 할 수있다. 이는 signal 이 sparse 하다는 가정을 기초로 한다. sparsity를 기반으로 L1-norm miniminzation을 이용해서 random measurements를 signal로 reconstruct하는 sensing matrix의 projections 평균에 의해 random measurements 를 이용한다. 해당 논문은 주어진 sparsifygin orthogonal을 기본으로 최소한의 일관성을 갖는 sensing matrics를 디자인 하는 방법을 제안한다. Noiselets 보다 나음을 위해 Biorthogonal bases를 이용한다. natural images 를 다룬 실험 결과로, Noiselets 보다 우수한 rate-distortion 결과를 보였다.
* Q is orthogonal if and only if Qᵀ is orthogonal. ( Q^-1 == Qᵀ 를 만족하는 정사각행렬 Q ) 혹은 QᵀQ == QQᵀ == I 로 알 수 있다. Qᵀ 는 transposed matrix (전치 행렬) 로써 주 대각선을 기준으로 뒤집은 행렬이다.
* Noiselet 은 wavelet 의 spread out domain 이다. (compact repsesentation in wavelents 으로 reconstruction이 가능하다.)
Introduction
Compressed Sensing
CS 는 sparsity 을 고려한 signal sample을 이용한다. 이 signal 은 알고있는 measurement function 이나 singal로 처리를 한다. Then, signal은 measurements의 subset에 해당된다. 측정값이 충분하다면 해당 measurements에 optimization algorithm을 이용하여 reconstruct를 할 수 있다.

CS를 할때 sensing matrix construction만들어야하는데 흔히는 단순히 randomly 만들어 사용한다. (결과가 낫밷)
Ψ : orthonormal basis
Φ : sensing matrix (M x N)
* basis : 일차독립이며 Span 하는 집합
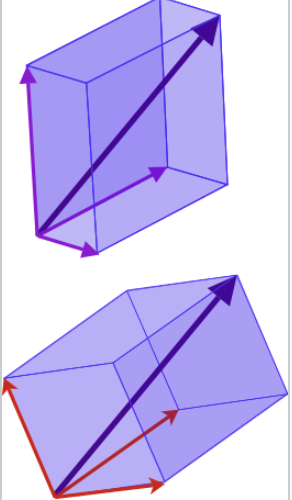

Constructing Sensing Matrices
해당 논문에서는 그냥 단순히 random sensing matrics가 아니라, basis Ψ 가 maximally incoherent 할 수 있도록 하는 measurement matrices Φ 를 구한다. 이는 다음과 같이 정리된다.
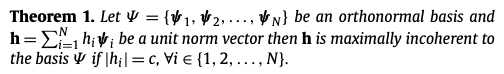
Ψ : orthonormal basis
h : unit norm vector
unit-norm vector h 가 largest angle 이자 가장 가까운 ±Ψj , j ∈ {1,2, ... N} 과 largest angle을 만들 때 maximally incoherent to an orthonormal basis Ψ 이다. Sensing Matrix Design 두가지 상황에서의 방법을 제시하였다. [1] maximally incoherent to a given orthogonal basis, [2] low coherence to a given biorthogonal basis.
Proposed construction for sensing matrices
모든 orthonormal basis 는 canonical basis 의 rotation이라고 볼 수 있다. 따라서, maximally incoherent Φ (M xN)를 구하기위해, canonical basis를 Ψ로 바꿀수 있는 rotation으로 M (linearly independent vectors)을 rotate 해야한다. 아래의 식을 이용해서 구할 수 있다.
Φ = HΨ
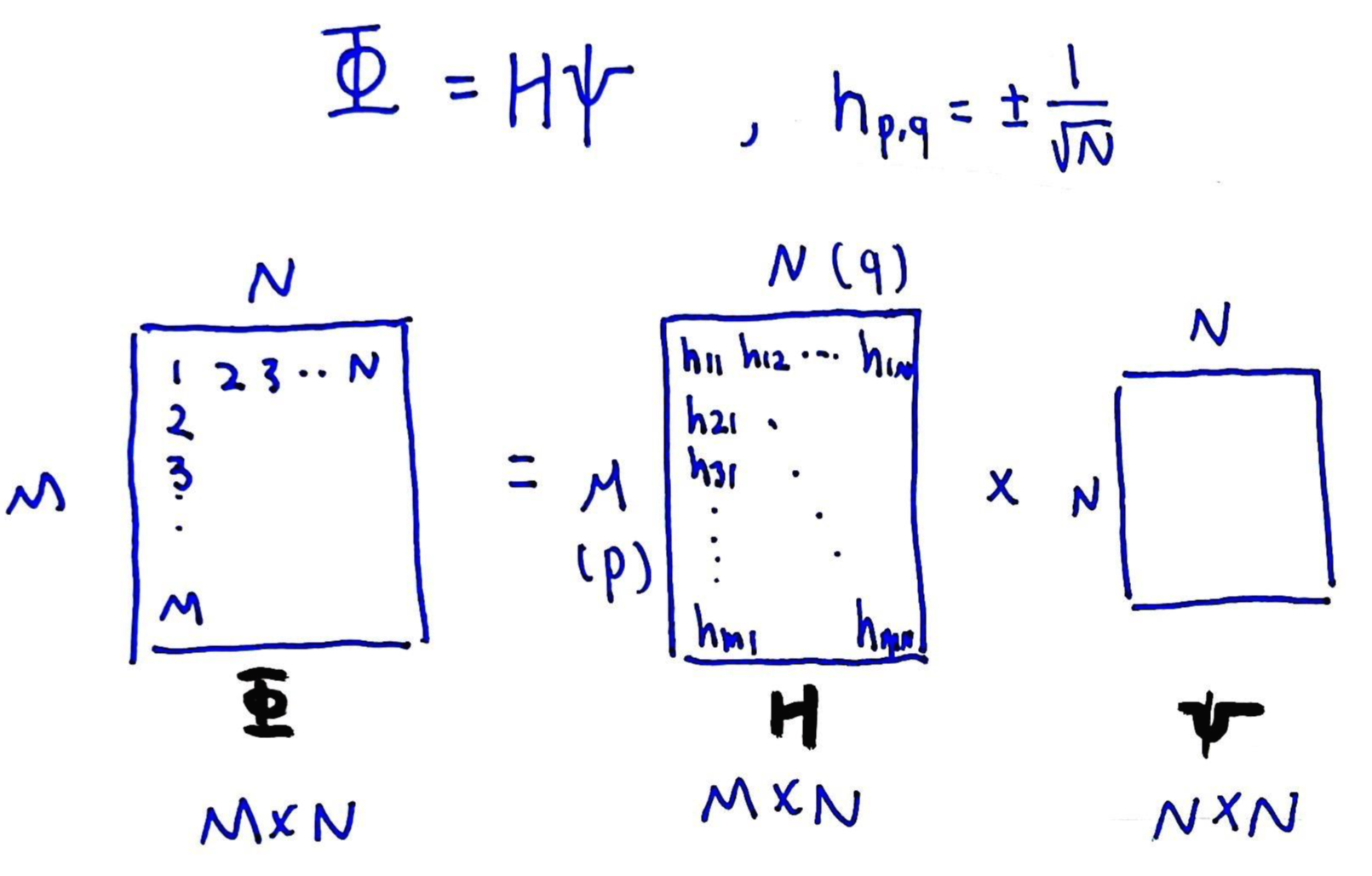
H 는 Hadamard matrix (N)에서 M개의 rows를 이용해서 만들 수 있다. 여기서 H 는 coherence 를 최소화 하기 위해 "constant absolute value coordinates" 를 만족해야한다.
* 해당 논문에서는 Hadamard, Noiselets 그리고 Gaussian sets를 이용해서 비교하였다.
Conclusion
Biorthogonal basis (locally maximally incoherenct sensing matrix ) 가 orthogonal basis (maximally incoherent sensing matrics) 보다 더 나은 rate-distortion 성과를 보였다. 이는 아마 이미지가 biorthogonal bases일때 더 sparse 하기 때문일 것이다.
Pereira, M. P., Lovisolo, L., da Silva, E. A. B., & de Campos, M. L. R. (2014). On the design of maximally incoherent sensing matrices for compressed sensing using orthogonal bases and its extension for Biorthogonal Bases Case. Digital Signal Processing, 27, 12–22. https://doi.org/10.1016/j.dsp.2014.01.006


