| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |
- 싱글셀 분석
- cellranger
- EdgeR
- Git
- python matplotlib
- scRNAseq analysis
- single cell rnaseq
- Bioinformatics
- CUTandRUN
- matplotlib
- github
- julia
- HTML
- ngs
- Batch effect
- js
- CUT&RUN
- single cell analysis
- scRNAseq
- drug development
- drug muggers
- javascript
- PYTHON
- MACS2
- 비타민 C
- single cell
- ChIPseq
- CSS
- DataFrame
- pandas
- Today
- Total
바이오 대표
[Leave-one-out] "Algebraic shortcuts for leave-one-out cross-validation in supervised network inference" 본문
[Leave-one-out] "Algebraic shortcuts for leave-one-out cross-validation in supervised network inference"
바이오 대표 2021. 11. 5. 01:32
- Leave-one-out CV(cross-validation)
- Two-step kernel regression
2. Supervised network prediction settings
[1] bipartite networks
[2] homogeneous networks
Issue
1) Symmetric 생각해주기 ex) protein u 가 protein v 랑 interaction 이 있으면 protein v 와 protein u 도 interaction
2) FN or missing interactions (없애보고 모델이 recover하는지 확인 필요 by zero-one-out)
2.1 Cross-validation for bipartite network prediction (protein-ligand interaction)
Four predictions
(1) the protein and the ligand both occur in the training network (I)
(2) only the protein occurs in the training network (R)
(3) only the ligand occurs in the training network (C)
(4) both vertices are new (B)
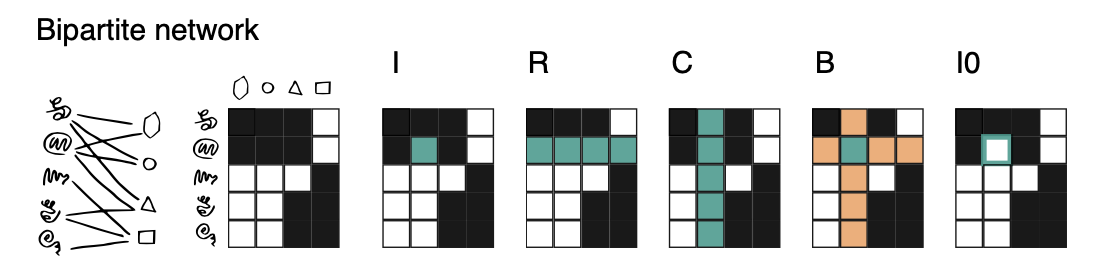

네가지의 prediction을 위 그림에서 I, R, C, B을 이용해서 할 수 있는데, training 할 때 input 값을 다르게 설정해주었다고 생각하면 된다. I 는 특정 Interactions 값들, R은 row 값들, C 는 columns들값, B는 row + column 값을 input 단위로 training 을 한다.
2.2 Cross-validation for homogeneous network prediction (protein-protein-interaction)
보통 symmetric 한 adjacency matrix 로 표현이 된다. (metabolic networks 는 skew-symmetric matrix)
* Symmetric Matrix(대칭 행렬) : 대각선을 기준으로 위와 아래가 대칭인 행렬 f (u, u′ ) = f (u′ , u)
* Skew-symmetric matrix: 대각선을 기준으로 위와 아래의 절대값이 대칭이지만 부호가 다른 행렬 f(u,u′) = −f(u′,u)
* Adjacency Matrix (인접 행렬): 노드(node)들의 연결관계(edge)를 나타내는 2차원 리스트
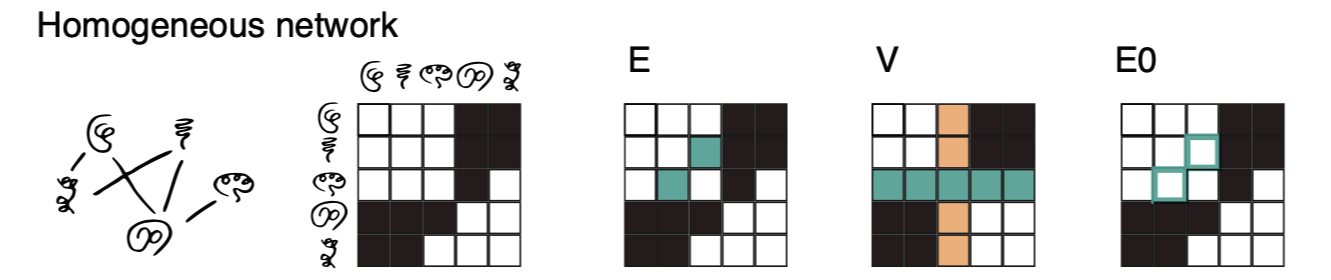

E는 대칭값을 함께 (u,v & v,u), V는 새로운 vertice가 network에서 어떻게 interaction을 하는지 알아볼때 사용된다.
* Here, every vertex is removed once from the net- work and the interaction values of the remaining vertices with this left-out vertex are predicted.
2.3 False negative interactions: leave-one-out versus zero-one-out
Biological network 에서는, interaction이 존재하지 않다고 나왔을 때 이를 증명할 수 있는 방법이 없기에, missing links in network는 정말 존재하지 않거나 (true negative) 존재하는데 나타나지 않거나 (false negative) 이다.
따라서 처음에 matrix의 모든 elements 값을 "0" 로 설정하고 변화는 주는 방식으로 training 을 진행한다.
3 Supervised network inference with two-step kernel ridge regression
Two-Step Kernel ridge regression, 쉽게 ridege regression 이 두번 실행 되었다고 생각하면 된다.
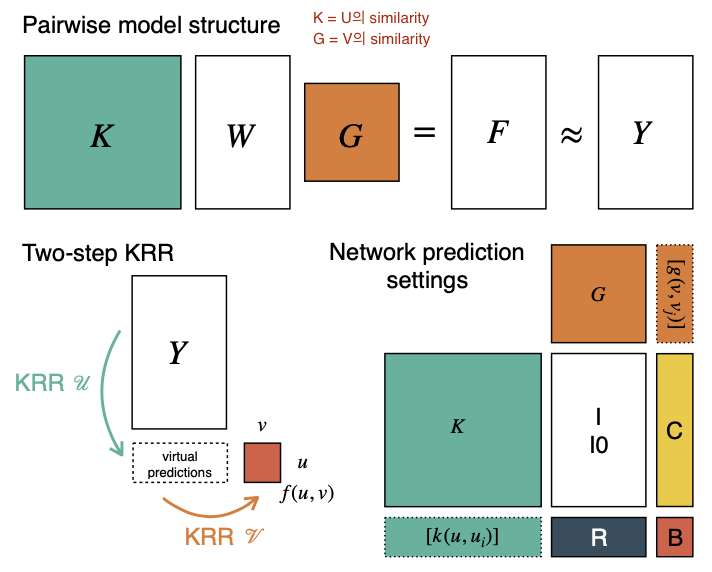
3.1 Predicting bipartite networks
K가 U 의 similairy matrix, G가 V의 similarity matrix 라고 할때, U&V의 interaction 은 다음과 같이 표현할 수 있다.
여기서 W는 weight matrix이다. ( I = identity matrix, λu and λv = regularization parameters )
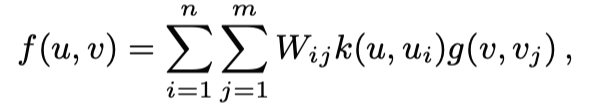
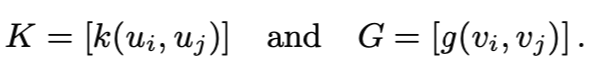
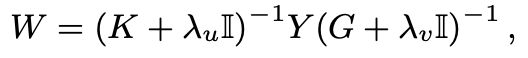
Eigenvalue decomposition 을 이용해서도 f(u,v)를 구할 수 있다. Pairwise kernel method O(n³m³) 보다 월등한 time complexity를 갖게 된다 O(n³+m³)
3.2 Predicting homogeneous networks
4 Shortcuts for leave-one-out cross-validation
4.1 Basic shortcuts for leave-one-out cross-validation
input 이 row 값이고 squared loss를 최소화 하는 모든 모델이 적용될 수 있다.

Reference
[1] Briefings in Bioinformatics, Volume 21, Issue 1, January 2020, Pages 262–271, https://doi.org/10.1093/bib/bby095




